摘要
本报告详细记录了Qwen3-8b-base模型在数学领域进行SFT（监督微调）和GRPO（组内归一化奖励策略优化）训练的过程、结果及相关分析。
训练旨在提升模型在数学问题解决方面的性能，特别是针对GSM8K和AIME24数据集。报告涵盖了环境配置、数据集准备、SFT训练阶段的损失曲线分析、GRPO训练阶段的关键指标变化，并总结了训练过程中遇到的挑战及解决方案。
1. 环境与硬件准备
为了进行Qwen3-8b-base模型的SFT和GRPO训练，配置了高性能的计算环境。
硬件方面，主要采用了8块4090显卡，每块显卡配备48GB显存，总计384GB显存，这为大型模型的训练提供了充足的计算资源。
在软件环境方面，我们参考了verl官方DAPO镜像hiyouga/verl:ngc-th2.6.0-cu126-vllm0.8.3，该镜像集成了所有必要的依赖，确保了训练环境的稳定性和兼容性。
具体配置如下：
- 硬件配置：8 * NVIDIA GeForce RTX 4090 (48GB GDDR6X)
- 推荐Docker镜像：
hiyouga/verl:ngc-th2.6.0-cu126-vllm0.8.3(集成了所有依赖)
在训练过程中，我们注意到显存占用是一个关键问题。
根据经验，使用BF16参数和FP32 Adam优化器进行全参数微调，且不使用梯度检查点（gradient checkpointing）时，所需的显存大约是模型参数量的7到8倍。对于7B模型，这可能需要高达100GB的显存。
因此，在实际操作中，我们通过调整micro-batch大小、使用param_offload以及临时缩短response_length等方法来优化显存使用，以避免训练过程中出现显存溢出（OOM）的问题。
2. 数据集：准备、去重与分层使用
高质量的数据集是模型训练成功的基石。本次训练中，我们针对SFT和RL（GRPO）阶段使用了不同的数据集，并进行了精心的准备和处理，包括数据去重和分层使用。
2.1 SFT 训练数据集
SFT阶段主要使用了数学领域的指令微调数据，旨在让模型学习解决数学问题的基本能力和格式，作为 cold start。具体数据集包括：
openai/gsm8k：简单的数学问题数据集。qingy2024/QwQ-LongCoT-Verified-130K：中等难度的数学问题数据集，包含prompt、解题步骤（CoT）和answer。
这些数据集经过处理，转换为prompt + cot + answer的格式，以适应模型的输入要求。在run_qwen3-8b-base.sh脚本中，SFT训练的数据源配置如下：
1data.train_files="[$HOME/data/gsm8k/train.parquet, $HOME/data/QwQ-LongCoT/train.parquet]"
2data.val_files="[$HOME/data/gsm8k/test.parquet]"
3data.prompt_key=prompt \
4data.response_key=answer
2.2 RL（GRPO）训练数据集
GRPO阶段主要使用了simplerl level5难度的数学题目，共约3k行数据。这些数据用于模型的强化学习，以进一步提升其在复杂数学问题上的推理和解决能力。验证集仍使用GSM8K-test。
2.3 数据预处理与去重
为了确保训练数据的质量和避免数据泄露，我们对数据集进行了预处理和去重操作。关键的去重策略是过滤掉与AIME的重叠数据，以保证测试集的独立性。具体实现方式如下：
1# 过滤 AIME
2def filter_overlap(example):
3 return example["source"] not in ["AIME", "AIME-II"]
4train_dataset = train_dataset.filter(filter_overlap)
数据转换完成后，目录结构示例如下：
data/
gsm8k/ train.parquet test.parquet
aime24/ test.parquet
...
2.4 奖励函数与 RewardManager 对接
在RL训练中，奖励函数的设计至关重要。对于数学类问题，我们统一使用了verl/utils/reward_score/math.py中的奖励函数。该函数通过抽取答案（格式为#### <数字或表达式>）并进行评分。如果没有按照格式输出则使用 flexible 答案匹配。
为了实现奖励函数的自动化路由，我们确保了parquet数据中的data_source字段取值为openai/gsm8k和aime24，RewardManager会根据这些字段自动选择或映射到相应的评分函数。
3. SFT 训练过程与结果分析
监督微调（SFT）是模型训练的第一阶段，旨在使Qwen3-8b-base模型初步具备理解和生成数学问题解决方案的能力。本阶段的训练主要基于run_qwen3-8b-base.sh脚本进行。
3.1 SFT 训练配置
SFT训练使用了torchrun启动，并配置了以下关键参数：
- 训练文件：
$HOME/data/gsm8k/train.parquet和$HOME/data/QwQ-LongCoT/train.parquet。 - 验证文件：
$HOME/data/gsm8k/test.parquet。 - Prompt Key：
prompt。 - Response Key：
answer。 - 每个GPU的微批次大小：
4。 - 最大序列长度：
2048。 - 模型路径：
$HOME/.cache/huggingface/hub/models--Qwen--Qwen3-8B-Base/snapshots/49e3418fbbbca6ecbdf9608b4d22e5a407081db4。 - LoRA Rank：
32，表明使用了LoRA（Low-Rank Adaptation）进行高效微调。 - 项目名称：
qwen3-8b-base-sft。 - 实验名称：
qwen3-8b-base-sft-2048。 - 总训练周期（Epochs）：
2。 - 日志记录器：
console和wandb。 - 每个节点的GPU数量：
8。
这些配置确保了训练能够充分利用硬件资源，并通过LoRA技术有效降低了训练成本。
3.2 SFT 训练结果分析
SFT训练的关键指标包括训练损失（train loss）、验证损失（validation loss）和学习率（learning rate）的变化。我们通过提供的图表对这些指标进行了分析。
3.2.1 验证损失 (sft_val_loss.png)
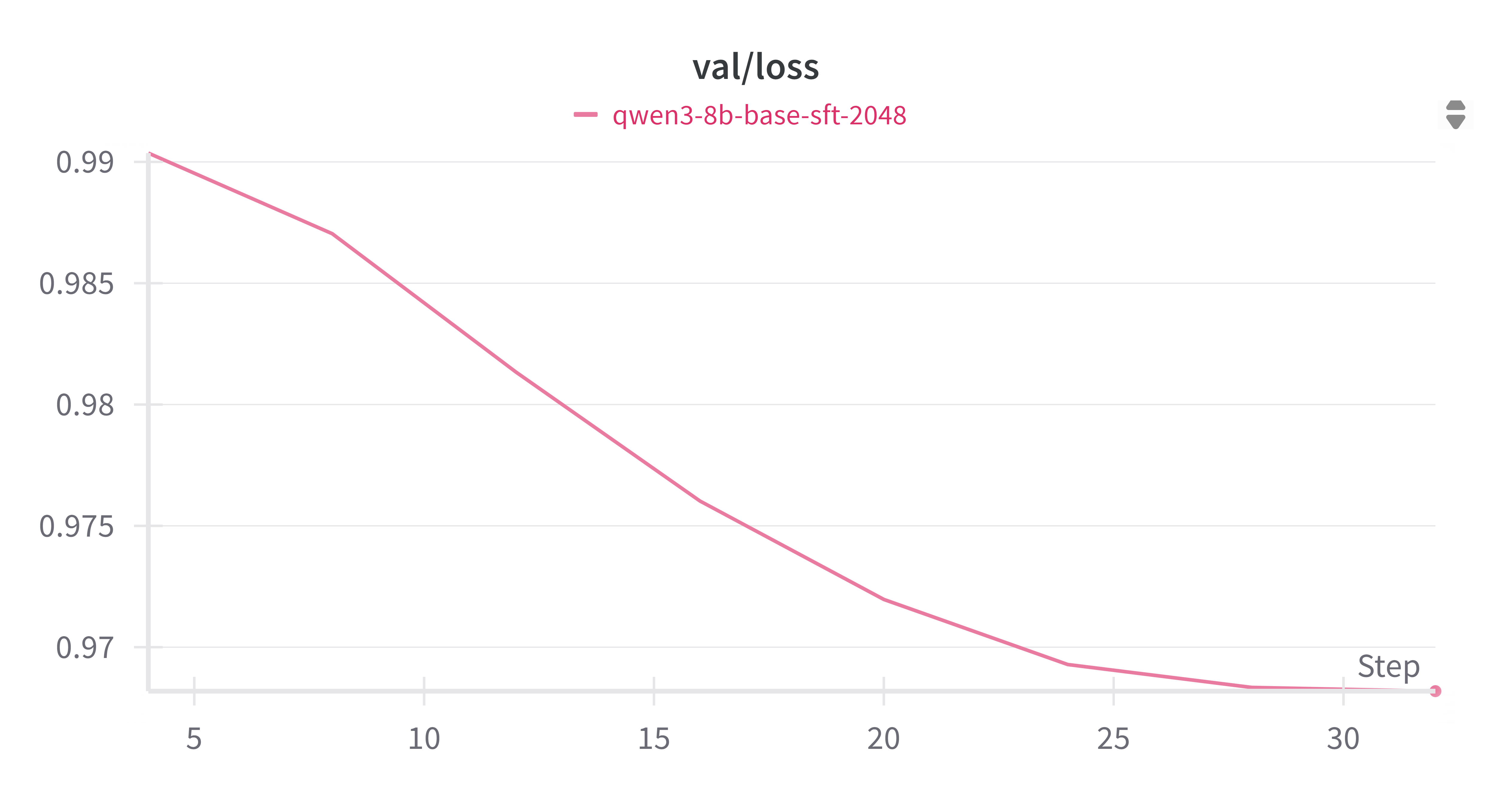
验证损失曲线（sft_val_loss.png）显示，随着训练步数的增加，验证损失呈现出持续下降的趋势。从初始的约0.99下降到最终的约0.965。这表明模型在未见过的验证集上表现良好，泛化能力逐渐增强，没有出现明显的过拟合迹象。损失的稳定下降是SFT阶段成功的关键指标，说明模型正在有效地从训练数据中学习。
3.2.2 训练损失 (sft_train_loss.png)
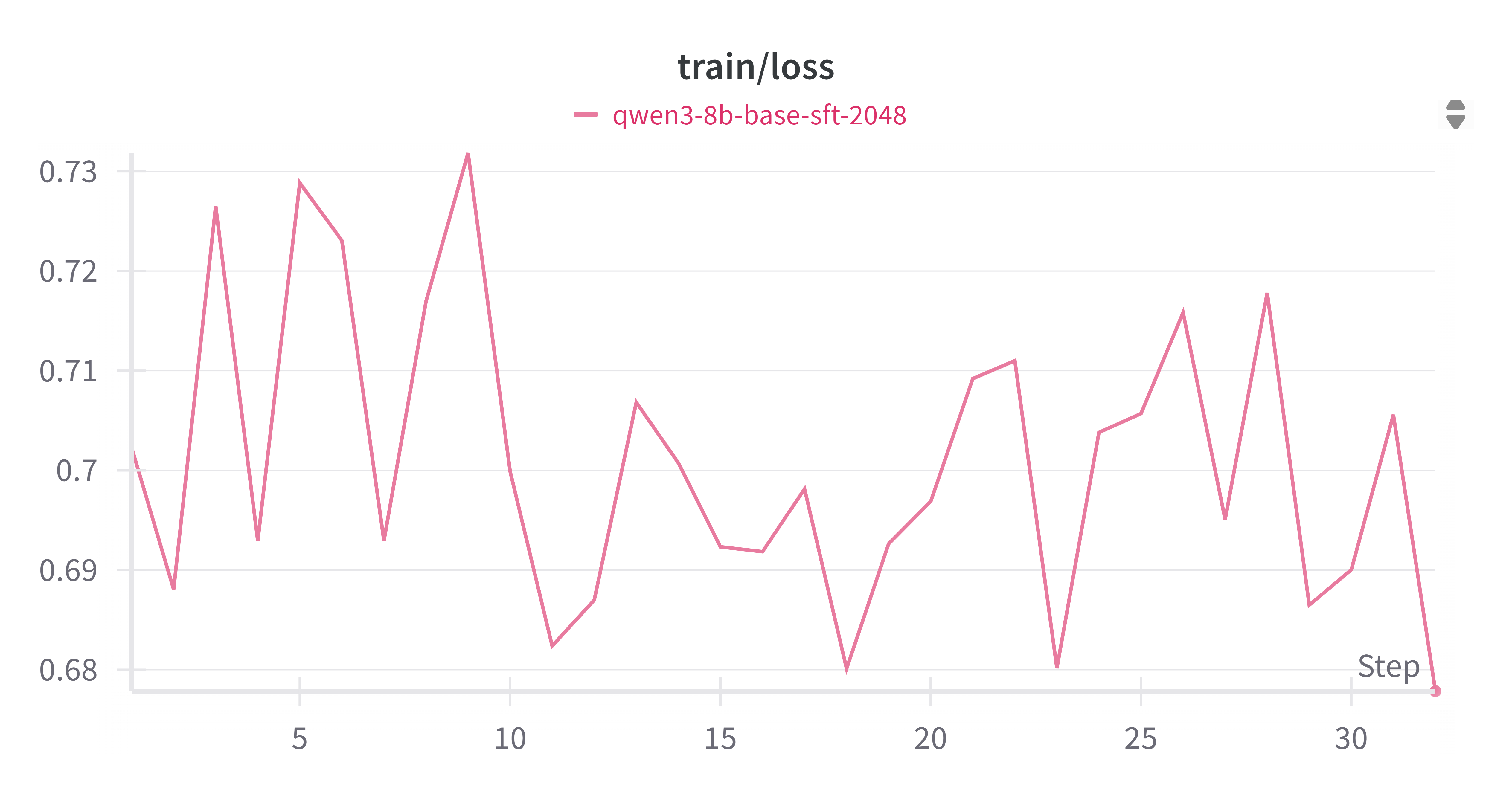
训练损失曲线（sft_train_loss.png）显示，训练损失在0.68到0.73之间波动。虽然存在一定的波动性，但整体趋势保持在一个相对稳定的范围内。训练损失的波动可能是由于数据批次之间的差异、梯度更新的随机性或者学习率调度策略等因素造成的。然而，考虑到验证损失的持续下降，这种训练损失的波动是可接受的，并且表明模型在训练集上持续学习。
3.2.3 学习率 (sft_train_lr.png)
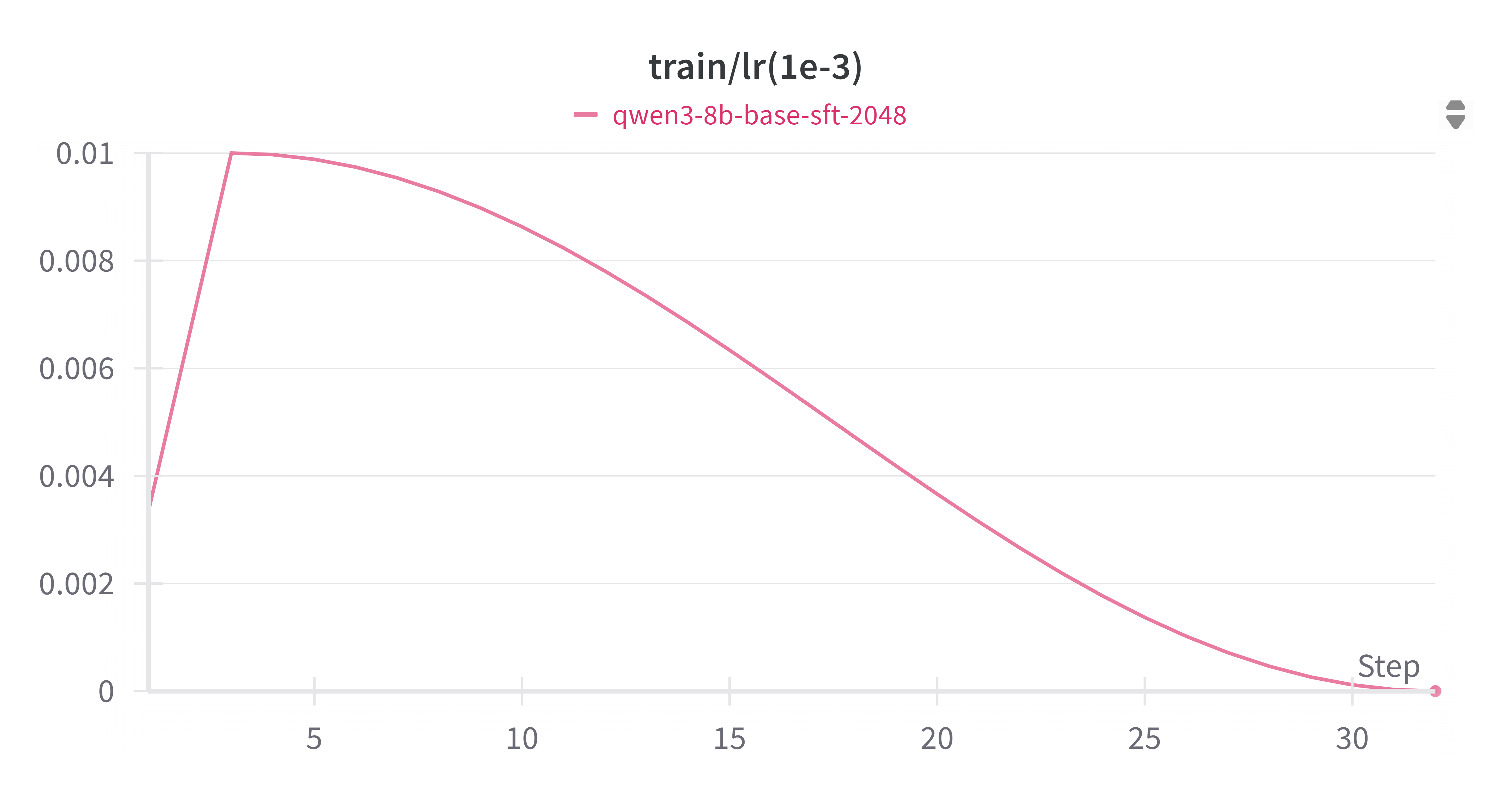
学习率曲线（sft_train_lr.png）显示，采用 warmup， 策略为余弦退火（cosine annealing）。预热阶段有助于模型在训练初期稳定学习，避免大的梯度震荡；随后的下降则有助于模型在训练后期更精细地收敛到最优解。这种学习率调度策略有助于SFT训练的稳定性和收敛性。
综上所述，SFT阶段的训练是成功的，模型在数学任务上表现出良好的学习能力，为后续的GRPO训练奠定了坚实的基础。
从验证集和测试集损失来看，模型有收敛的趋势，继续训练可以继续收敛，但是 SFT 阶段仅仅作为 cold start 并不要求模型达到收敛点。
验证集上损失的收敛更多受到学习率的影响。
4. GRPO 训练过程与结果分析
在SFT训练完成后，我们进入了GRPO（Group-wise Reward Policy Optimization）训练阶段。GRPO是一种基于强化学习的策略优化算法，旨在通过优化奖励函数来进一步提升模型在特定任务上的性能。本阶段的训练主要基于run_qwen3-8b_simplerl_grpo_lora.sh脚本进行。
4.1 GRPO 训练配置
GRPO训练使用了python3 -m verl.trainer.main_ppo命令启动，并配置了以下关键参数：
- 算法：
algorithm.adv_estimator=grpo，明确使用GRPO算法。 - 训练文件：
$HOME/data/simplerl/train.parquet，使用simplerl level5难度题目。 - 验证文件：
$HOME/data/gsm8k/test.parquet。 - 训练批次大小：
data.train_batch_size=32。 - 最大Prompt长度：
data.max_prompt_length=1024。 - 最大Response长度：
data.max_response_length=8192。 - 模型路径：
actor_rollout_ref.model.path=$HOME/.cache/huggingface/hub/models--Qwen--Qwen3-8B/snapshots/9c925d64d72725edaf899c6cb9c377fd0709d9c5。 - LoRA Rank：
actor_rollout_ref.model.lora_rank=64，LoRA Alpha：actor_rollout_ref.model.lora_alpha=32。 - Actor优化器学习率：
actor_rollout_ref.actor.optim.lr=5e-7。 - PPO Mini Batch Size：
actor_rollout_ref.actor.ppo_mini_batch_size=8。 - PPO Micro Batch Size Per GPU：
actor_rollout_ref.actor.ppo_micro_batch_size_per_gpu=2。 - KL散度损失：
actor_rollout_ref.actor.use_kl_loss=True，KL损失系数0.001。 - 梯度检查点：
actor_rollout_ref.model.enable_gradient_checkpointing=True。 - 参数卸载：
actor_rollout_ref.actor.fsdp_config.param_offload=False，actor_rollout_ref.ref.fsdp_config.param_offload=True。 - Rollout配置：
actor_rollout_ref.rollout.max_num_batched_tokens=32748，actor_rollout_ref.rollout.tensor_model_parallel_size=4，actor_rollout_ref.rollout.gpu_memory_utilization=0.6。 - 项目名称：
qwen3-8b-grpo。 - 实验名称：
qwen3-8b_simplerl_grpo_lora。 - 每个节点的GPU数量：
8。
这些配置反映了GRPO训练的复杂性，包括对显存的精细控制（如param_offload和gpu_memory_utilization），以及对RL特定参数（如KL损失、PPO批次大小）的调整。
4.2 GRPO 训练结果分析
GRPO训练阶段的关键指标包括KL损失、Critic分数、验证集奖励均值、PG损失和Critic回报均值。我们通过提供的图表对这些指标进行了分析。
4.2.1 Actor KL Loss (grpo_kl_loss.png)
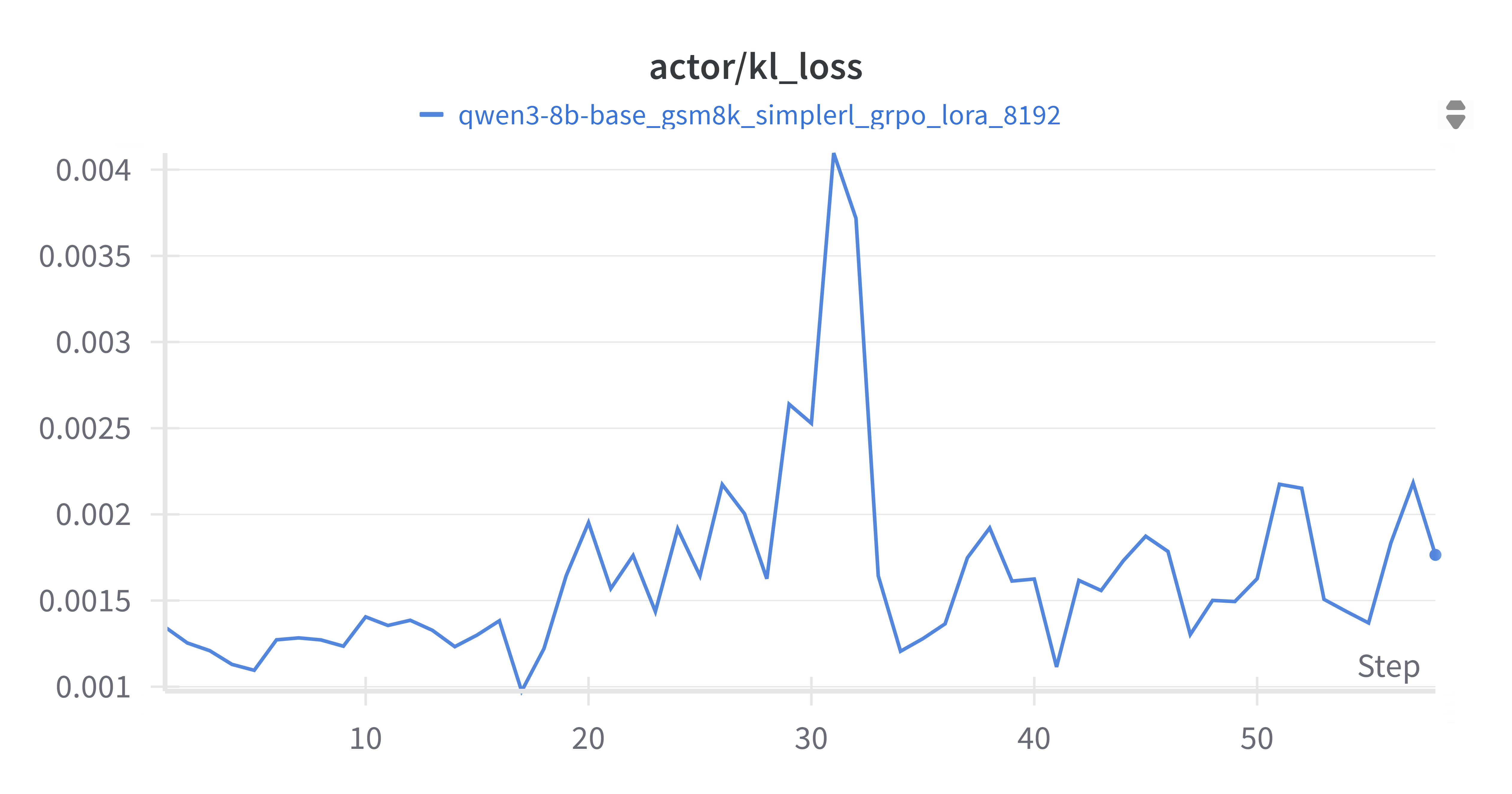
Actor KL损失（grpo_kl_loss.png）衡量了当前策略与参考策略之间的KL散度。从图中可以看出，KL损失在训练过程中呈现波动，但整体保持在较低水平（0.001到0.004之间）。KL损失的波动性是RL训练中常见的现象，但其保持在合理范围内表明策略更新没有偏离参考策略太远，有助于训练的稳定性。
4.2.2 Critic Score Mean (grpo_critic_score_mean.png)
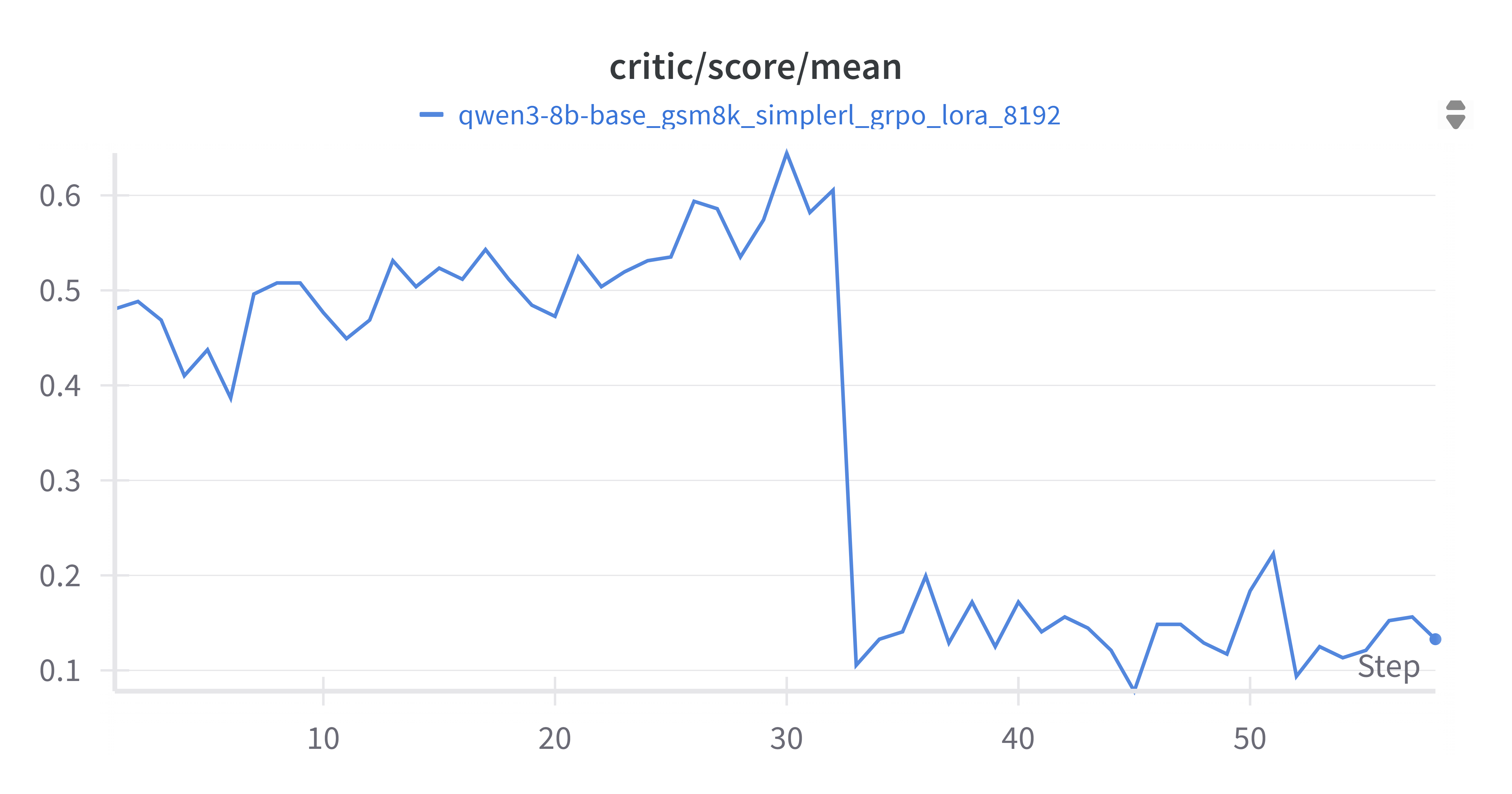
Critic分数均值（grpo_critic_score_mean.png）反映了Critic网络对当前状态价值的估计。在训练初期，Critic分数均值在0.4到0.6之间波动，但在大约30步之后，出现了一个显著的下降，随后稳定在0.1到0.2之间。
这里critic下降与训练数据集中的难度切换对应，数据集中样本此时从简单的 gsm8k 换到 simplerl 的level=5， 样本的难度，prompt length都有所增加。
4.2.3 Validation Mean Reward (grpo_val_mean@1.png)
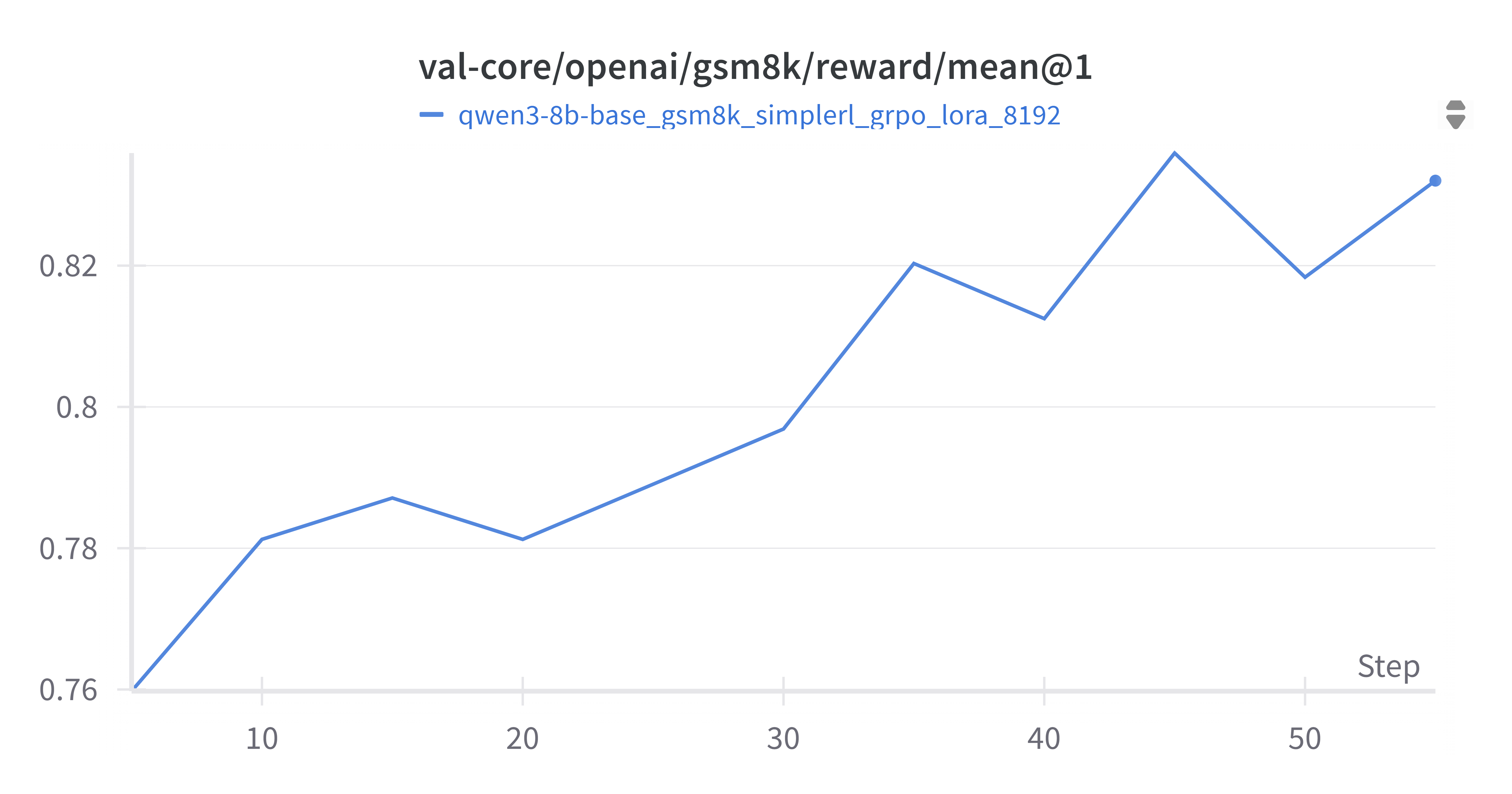
验证集奖励均值（grpo_val_mean@1.png）是衡量模型在未见过数据上性能的关键指标。从图中可以看出，验证集奖励均值呈现出稳步上升的趋势，从初始的约0.76上升到最终的约0.83。这表明GRPO训练有效地提升了模型在数学问题解决上的性能，模型能够生成更高质量的答案，从而获得更高的奖励。这是GRPO训练成功的直接证据。
4.2.4 Actor PG Loss (grpo_pg_loss.png)
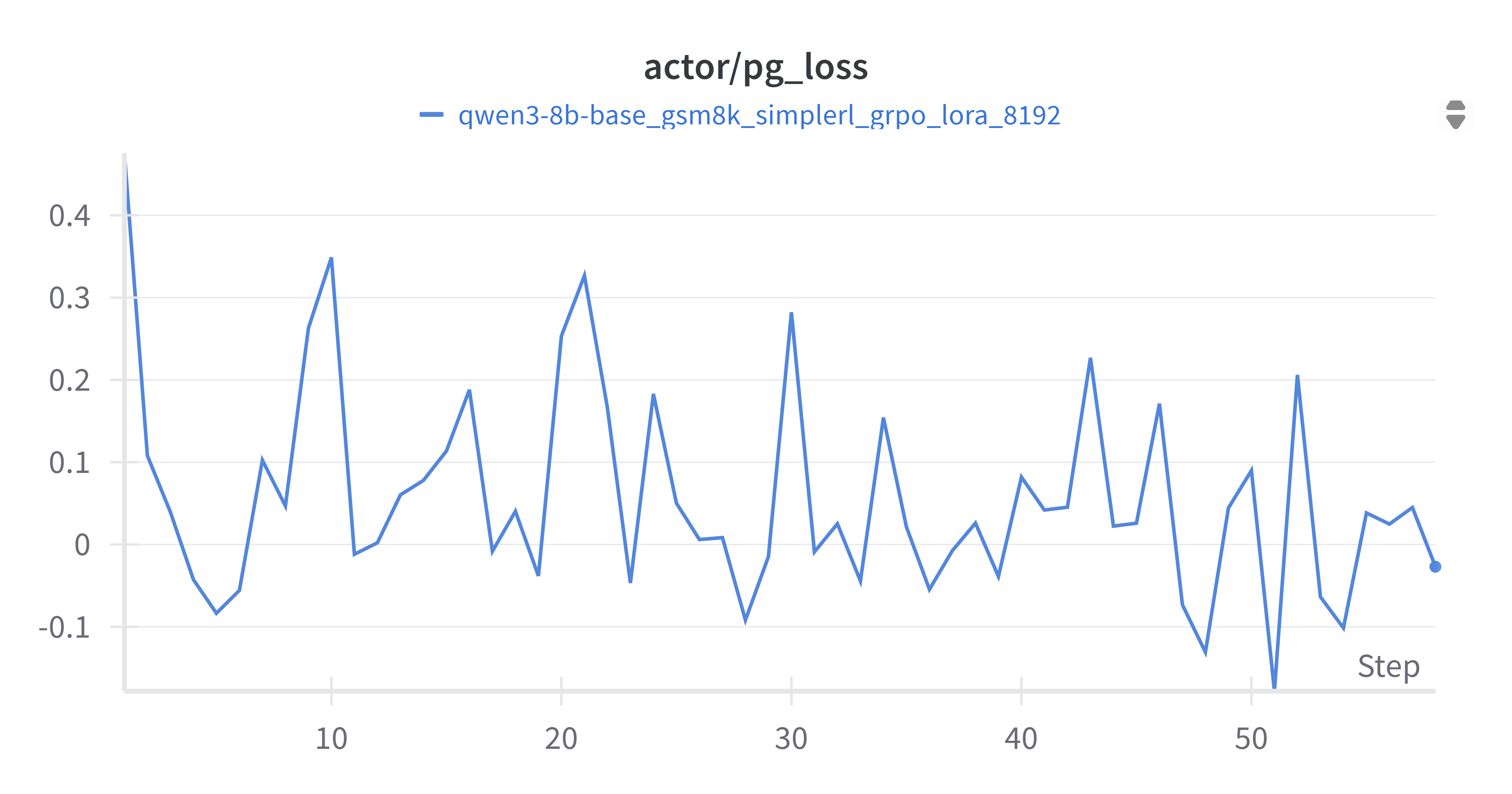
Actor PG损失（grpo_pg_loss.png）是策略梯度损失，用于更新Actor网络。从图中可以看出，PG损失在训练过程中波动剧烈，在正负之间交替。这种波动性是策略梯度算法的典型特征，因为策略梯度是基于蒙特卡洛估计的，具有较高的方差。尽管波动，但PG损失的优化最终导致了验证集奖励的提升，说明策略梯度更新是有效的。
4.2.5 Critic Returns Mean (grpo_critic_returns_mean.png)
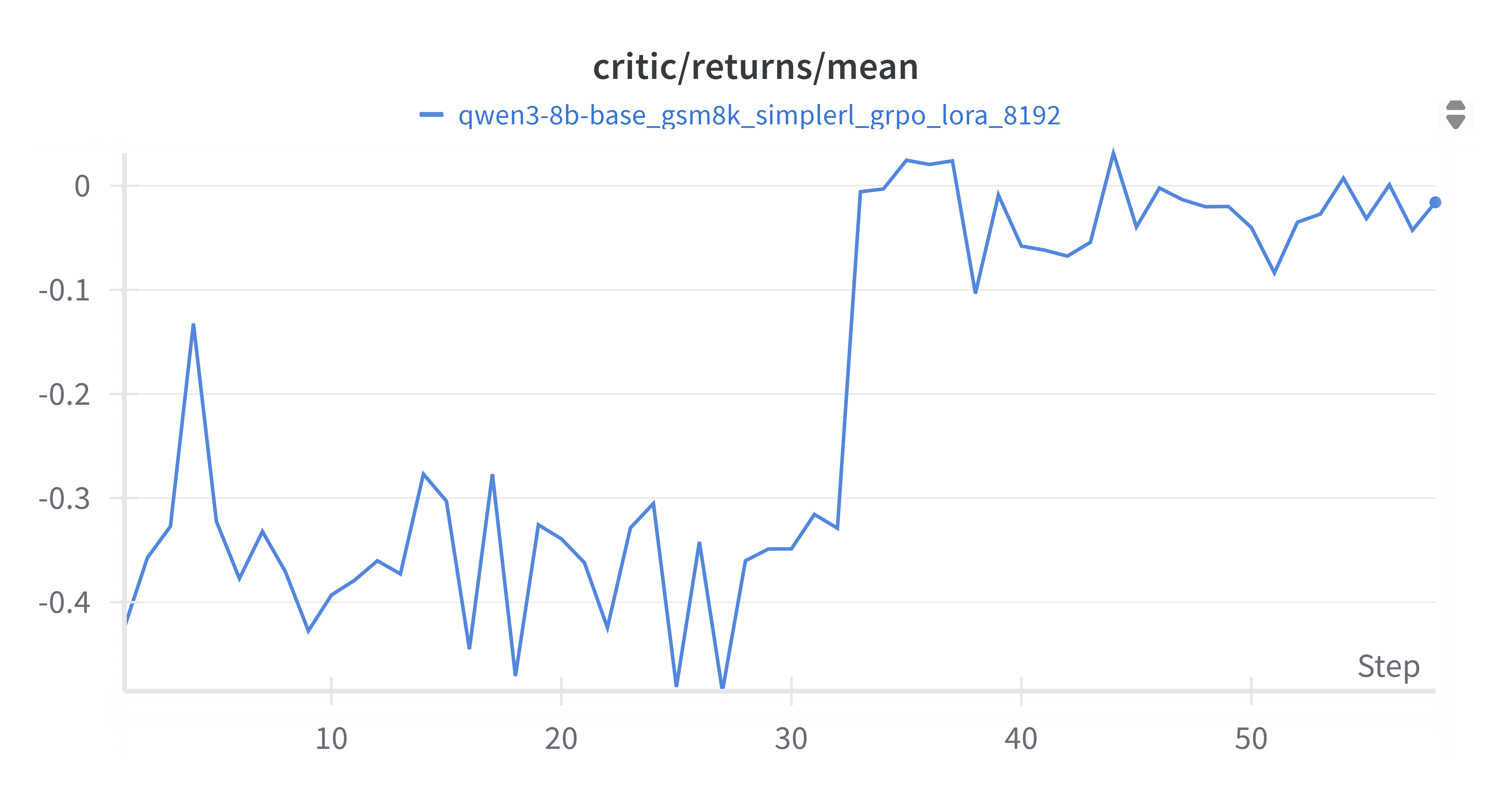
Critic 回报均值（grpo_critic_returns_mean.png）反映了Critic网络估计的累积回报。与Critic分数均值类似，Critic回报均值在训练初期在-0.4到0之间波动，但在大约30步之后，出现了一个显著的上升，随后稳定在0到0.05之间。这与Critic分数均值的变化趋势一致，可能反映了Critic网络对未来回报的估计变得更加积极或准确。
5. 最终评测结果
为了全面评估SFT和GRPO训练对Qwen3-8b-base模型性能的影响，我们在GSM8K和AIME24两个数学基准测试集上进行了评测。评测结果如下表所示：
| 模型 | GSM8K | AIME24 | AIME24② | 分析 |
|---|---|---|---|---|
| Qwen3-8B-Base | 61.92 | 0 | 10 | 基础模型在AIME24上存在复读问题，并且由于没有完全遵守回答格式，部分正确回答miss。在②中准确率为加上miss正确答案后的准确率 |
| +sft | 63.48 | 0 | 13.3 | SFT后GSM8K性能略有提升，但AIME24问题依旧 |
| +sft+grpo | 83.59 | 10 | 16.7 | GRPO后GSM8K性能显著提升，并有效缓解了AIME24上的复读现象。模型更加遵守输出格式 |
从评测结果可以看出：
- 基础模型（Qwen3-8B-Base） 在GSM8K上表现尚可，但在更具挑战性的AIME24上完全无法得分，并存在复读问题。
- SFT训练后（Qwen3-8B-Base-sft），模型在GSM8K上的性能有小幅提升，但AIME24上的问题没有得到解决。
- GRPO训练后（Qwen3-8B-Base-sft-grpo），模型在GSM8K上的性能取得了显著的飞跃，从63.48提升到83.59。更重要的是，GRPO训练有效缓解了模型在AIME24上的复读现象，并取得了16.7分的成绩。这表明GRPO训练不仅提升了模型的数学推理能力，还改善了其生成行为，使其能够更好地应对复杂问题。
5.1 在aime24数据集上对 Base 与 RL后模型输出的分析
检查在Base中错误但是rl训练后正确的题目：14，19
14：Find the largest possible real part of $(75+117i)z+\frac{96+144i}{z}$ where $z$ is a complex number with $|z|=4$.
| 维度 | Base 模型 ① | GRPO 模型 ② |
|---|---|---|
| 最终答案 | 600（错误） | 540（正确） |
| 实部化简 | 把表达式错误化成$$Re[(75+117i)z]+Re[(96+144i)/z]$$ 关键一步出错： $(75 + 117i)(4cos \theta + 4sin\theta i) $ $+ (24cos\theta + 36sin\theta i + 36cos\theta + 24sin\theta i)$ $= (360cos\theta + 528sin\theta)$ $+ (360sin\theta - 528cos\theta)i$ → 系数360, 528都偏大； → $i^2=-1$没有正确处理； |
得到$\operatorname{Re}=324\cos\theta+432\sin\theta$ 但是正确表达式为 $\operatorname{Re}=324\cos\theta-432\sin\theta$ |
| 求最大值方法 | 直接给出最大值时的$cos\theta$ $$cos\theta = \frac{528}{\sqrt{360^2 + 528^2}} = \frac{528}{\sqrt{435360}} = \frac{132}{119}$$ 但把$\sqrt{360^2+528^2}$近似拆成 “132/119、90/119” 等错误三角值（>1） |
$\max= \sqrt{324^2+432^2}=540$， 并给出$$\cos\theta=\tfrac35,;\sin\theta=\tfrac45$$ |
① 在进行乘法时没有正确处理虚数平方，系数前后不一致 ② 求取实部没有正确处理虚数平方，但是上下系数一致
① 的三角替换数值超界，还掩盖了前面系数错位；② 前面公式推理不正确，但是很巧两个公式最大值都是$540$。
19：Find the number of triples of nonnegative integers $(a,b,c) $ satisfying $$(a + b + c )= 300 $$ and $$a^2b + a^2c + b^2a + b^2c + c^2a + c^2b = 6,000,000$$
| 维度 | GRPO 模型 ① | Base 模型 ② |
|---|---|---|
| 最终答案 | 给出601，与真值一致 | 给出0 |
| 关键化简 | 正确利用 1. 对称多项式恒等式 $a^3+b^3+c^3−3abc$$=(a+b+c)(a^2+b^2+c^2−ab−bc−ca)$ 2. 代入 $a+b+c=300$ 后推到$50(a^2+b^2+c^2)+abc=2500000$ |
关键一步为$6 000 000=(a+b+c)(ab+ac+bc)−3abc$ 随后推导出 $a^2 + b^2 + c^2 $$= 90000 - (12000000 + 6 * abc) / 300$ |
| 枚举策略 | 利用$a+b+c=300$限制：双层循环a,b，直接算c，并按等式检验 | 先推导再检验 “$a^2+b^2+c^2$是否为整数”，实际判定条件与原方程无直接对应；又用float.is_integer() 判整→ 数值精度隐患；最终因判定式错误得到 0 |
代码1 - GRPO模型方法：
1count = 0
2for a in range(301):
3 for b in range(301 - a):
4 c = 300 - a - b
5 if 50 * (a**2 + b**2 + c**2) + a * b * c == 2500000:
6 count += 1
7print(count)
代码2 - Base模型方法：
1count = 0
2for a in range(301):
3 for b in range(301 - a):
4 c = 300 - a - b
5 abc = a * b * c
6 a2_b2_c2 = 90000 - (12000000 + 6 * abc) / 300
7 if a2_b2_c2.is_integer() and a2_b2_c2 >= 0:
8 count += 1
9print(count)
两者在关键化简部分数学推导过程不同，但最终等式等价。 Base 模型可能已具备初步数学推理能力
在后面的枚举策略中 ① 方法简单却稳妥 ② 算法与数学约束脱节，没有判定相等，自己虚构判定指标。
观察和思考
- Base模型和RL后模型都展现出正确求解思路；但是在公式化简步骤中容易出现错误，最常见是（符号丢失 / 系数乘错 / 括号漏写）；
- 但Base模型在上下公式推导一致性，系数和符号处理上容易出错，导致后续推理链条破裂；
- RL 训练能够提高公式、系数和符号的处理上准确性；
- 尝试sft或者rl阶段增加按步骤的公式推导可能能够增加推理数学公式推理准确性；
- 少量、针对性的 SFT 数据——哪怕只是简单恒等式推导或单位系数练习——也可能带来显著收益
6. 结论与展望
本次针对Qwen3-8b-base模型的SFT+GRPO训练取得了显著的成功。通过结合监督微调和强化学习两种训练范式，我们成功地提升了模型在数学问题解决方面的性能，特别是在GSM8K和AIME24数据集上取得了优异的成绩。
SFT阶段为模型注入了必要的数学知识和解题格式，而GRPO阶段则通过优化奖励函数，进一步对齐了模型的行为，使其能够生成更高质量、更准确的答案。训练过程中的各项指标分析也为我们提供了宝贵的经验，例如学习率调度策略的重要性、KL散度在稳定RL训练中的作用，以及验证集奖励在评估模型性能方面的关键意义。
附录：训练心得
- 显存估计：对训练占用显存有一个基础的估计。参数使用bf16，使用adam优化器fp32，不使用gradient checkpoint，全参量微调，需要7~8倍参数量大小的显存。例如，7B模型大约需要100G显存。
- 调整输出序列长度：在训练过程中，应从小到大慢慢调整
output_seq_len，尽量提高显存利用率。 - 配置常见问题：训练过程中会遇到训练参数配置问题，需要根据具体情况进行代码排查和解决。如 vLLM 在profill 阶段对
max_num_batched_tokens限制 - 日志与指标监控非常关键：在SFT与GRPO阶段，应持续记录和分析以下指标：loss、KL散度、reward、learning rate、gradient norm 等。使用 wandb 实时可视化，有助于快速定位训练异常或超参选择不当的问题。