Summary
This report details the process, results, and analysis of SFT (Supervised Fine-tuning) and GRPO (Group-wise Reward Policy Optimization) training of the Qwen3-8b-base model in the mathematical domain.
The training aims to enhance the model’s performance on mathematical problem-solving, especially for the GSM8K and AIME24 datasets. The report covers environment setup, dataset preparation, loss curve analysis for the SFT stage, key metric changes during the GRPO stage, and challenges encountered with corresponding solutions.
1. Environment and Hardware Setup
To train the Qwen3-8b-base model with SFT and GRPO, a high-performance computing environment was configured.
On the hardware side, we used eight RTX 4090 GPUs, each with 48GB of VRAM, totaling 384GB. This provided sufficient resources for large-scale model training.
For the software environment, we used the official verl DAPO Docker image hiyouga/verl:ngc-th2.6.0-cu126-vllm0.8.3, which integrates all required dependencies and ensures stability and compatibility.
Configuration Summary:
- Hardware: 8 × NVIDIA GeForce RTX 4090 (48GB GDDR6X)
- Recommended Docker Image:
hiyouga/verl:ngc-th2.6.0-cu126-vllm0.8.3
Memory usage was a key concern during training. Based on experience, BF16 parameters and FP32 Adam optimizer in full-parameter fine-tuning without gradient checkpointing may require 7–8× the model parameter size in memory. For a 7B model, this may exceed 100GB.
Thus, we optimized memory usage through methods like adjusting micro-batch size, enabling parameter offloading, and temporarily shortening response length to avoid OOM errors.
2. Dataset: Preparation, Deduplication, and Usage Strategy
High-quality datasets are fundamental to successful model training. We used different datasets for the SFT and RL (GRPO) phases, along with deduplication and tiered usage strategies.
2.1 SFT Training Dataset
In the SFT phase, we used math-domain instruction tuning data to teach the model basic problem-solving skills and formats, serving as a cold start. The datasets include:
openai/gsm8k: Simple math problemsqingy2024/QwQ-LongCoT-Verified-130K: Moderately difficult problems with prompts, chain-of-thought (CoT), and answers
We formatted these datasets as prompt + cot + answer. The configuration in run_qwen3-8b-base.sh is:
1data.train_files="[$HOME/data/gsm8k/train.parquet, $HOME/data/QwQ-LongCoT/train.parquet]"
2data.val_files="[$HOME/data/gsm8k/test.parquet]"
3data.prompt_key=prompt
4data.response_key=answer
2.2 RL (GRPO) Training Dataset
The GRPO phase used approximately 3,000 simplerl level5 math questions to improve the model’s reasoning on complex tasks. The validation set remained GSM8K-test.
2.3 Preprocessing and Deduplication
To ensure data quality and prevent data leakage, we deduplicated datasets by filtering out overlaps with AIME. For example:
1# Filter AIME data
2def filter_overlap(example):
3 return example["source"] not in ["AIME", "AIME-II"]
4train_dataset = train_dataset.filter(filter_overlap)
Post-processing, the data directory looked like:
data/
gsm8k/ train.parquet test.parquet
aime24/ test.parquet
...
2.4 Reward Function and RewardManager Integration
Reward design is crucial in RL training. For math tasks, we used the reward function in verl/utils/reward_score/math.py, which extracts and scores answers formatted as #### <number or expression>. Flexible matching is applied if the output is not formatted.
To automate reward routing, we ensured the data_source field in the parquet files matched the reward function (e.g., openai/gsm8k, aime24).
3. SFT Training Process and Analysis
SFT is the initial training stage, aimed at equipping the model with the ability to understand and generate math solutions. We used run_qwen3-8b-base.sh to launch training.
3.1 SFT Training Configuration
Training was launched via torchrun with key parameters:
- Train Files:
gsm8kandQwQ-LongCoT - Validation File:
gsm8k test set - Prompt Key:
prompt - Response Key:
answer - Micro-Batch per GPU: 4
- Max Sequence Length: 2048
- Model Path: HuggingFace snapshot
- LoRA Rank: 32
- Project/Experiment Names:
qwen3-8b-base-sft,qwen3-8b-base-sft-2048 - Epochs: 2
- Loggers:
console,wandb - GPUs per Node: 8
These settings helped maximize hardware efficiency and reduced costs via LoRA fine-tuning.
3.2 SFT Training Results
We tracked three key metrics: train loss, validation loss, and learning rate.
3.2.1 Validation Loss
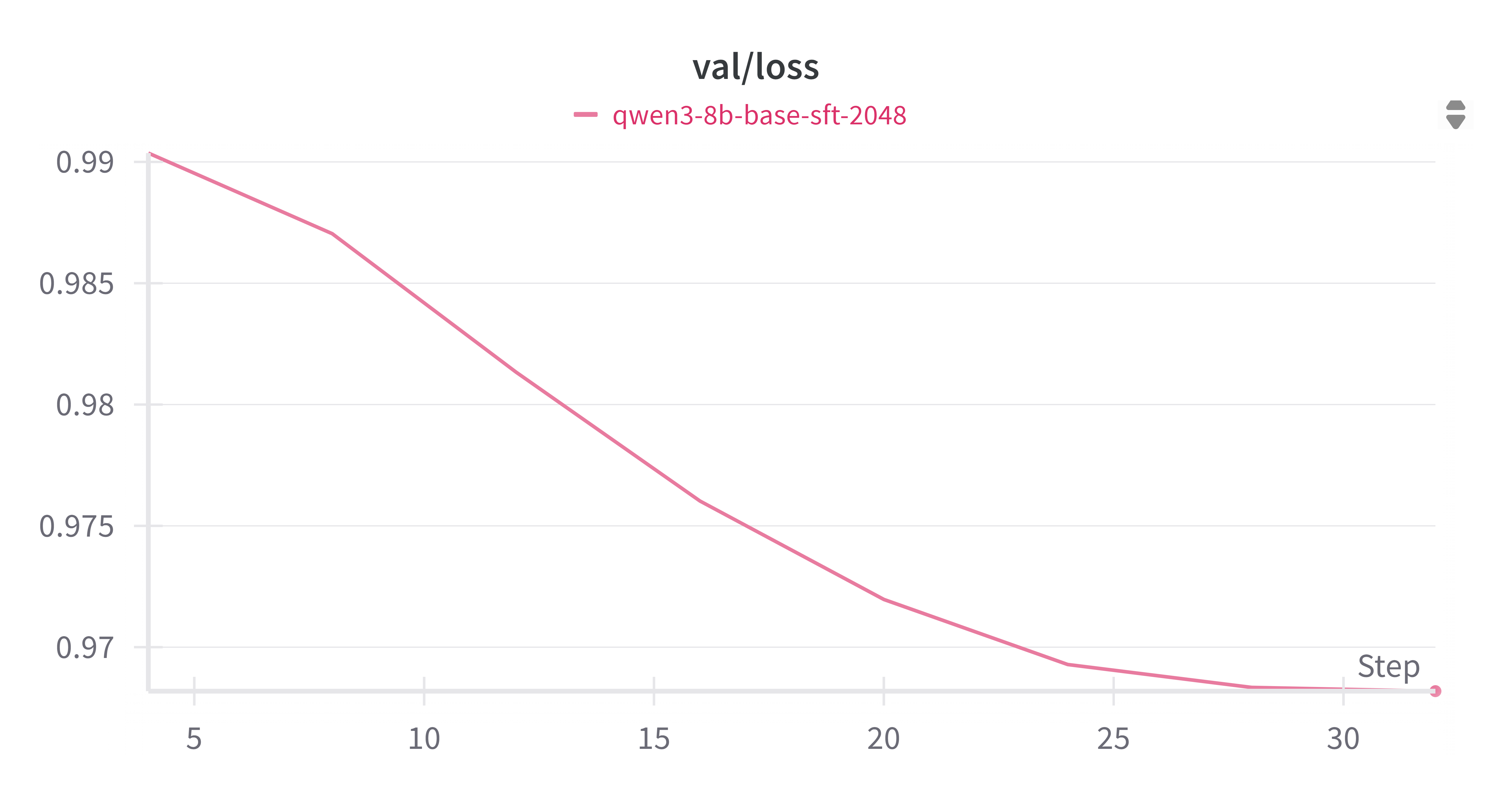
Validation loss steadily dropped from ~0.99 to ~0.965, indicating improved generalization with no overfitting.
3.2.2 Training Loss
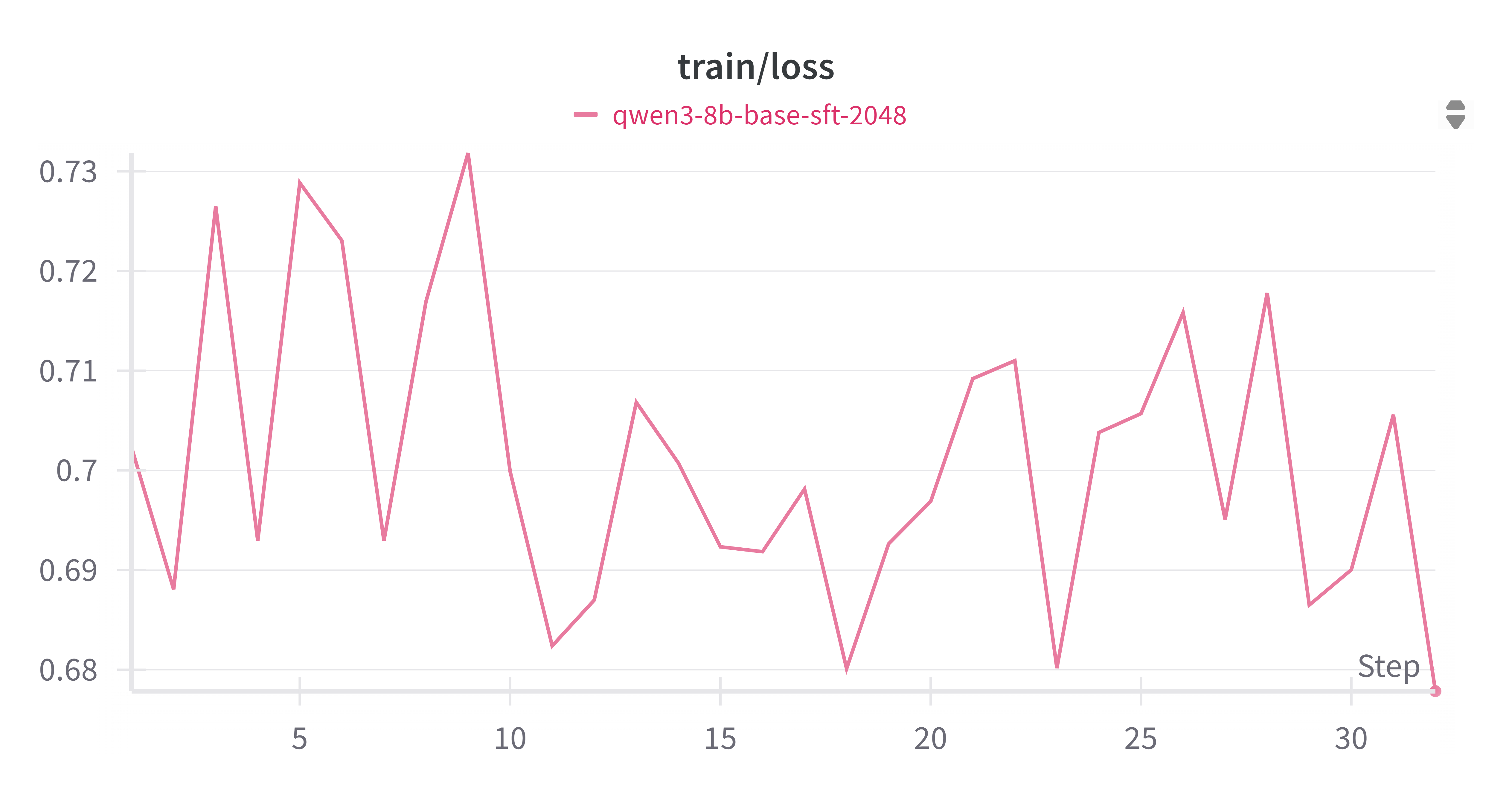
Training loss fluctuated between 0.68–0.73, which is acceptable considering validation loss steadily improved.
3.2.3 Learning Rate
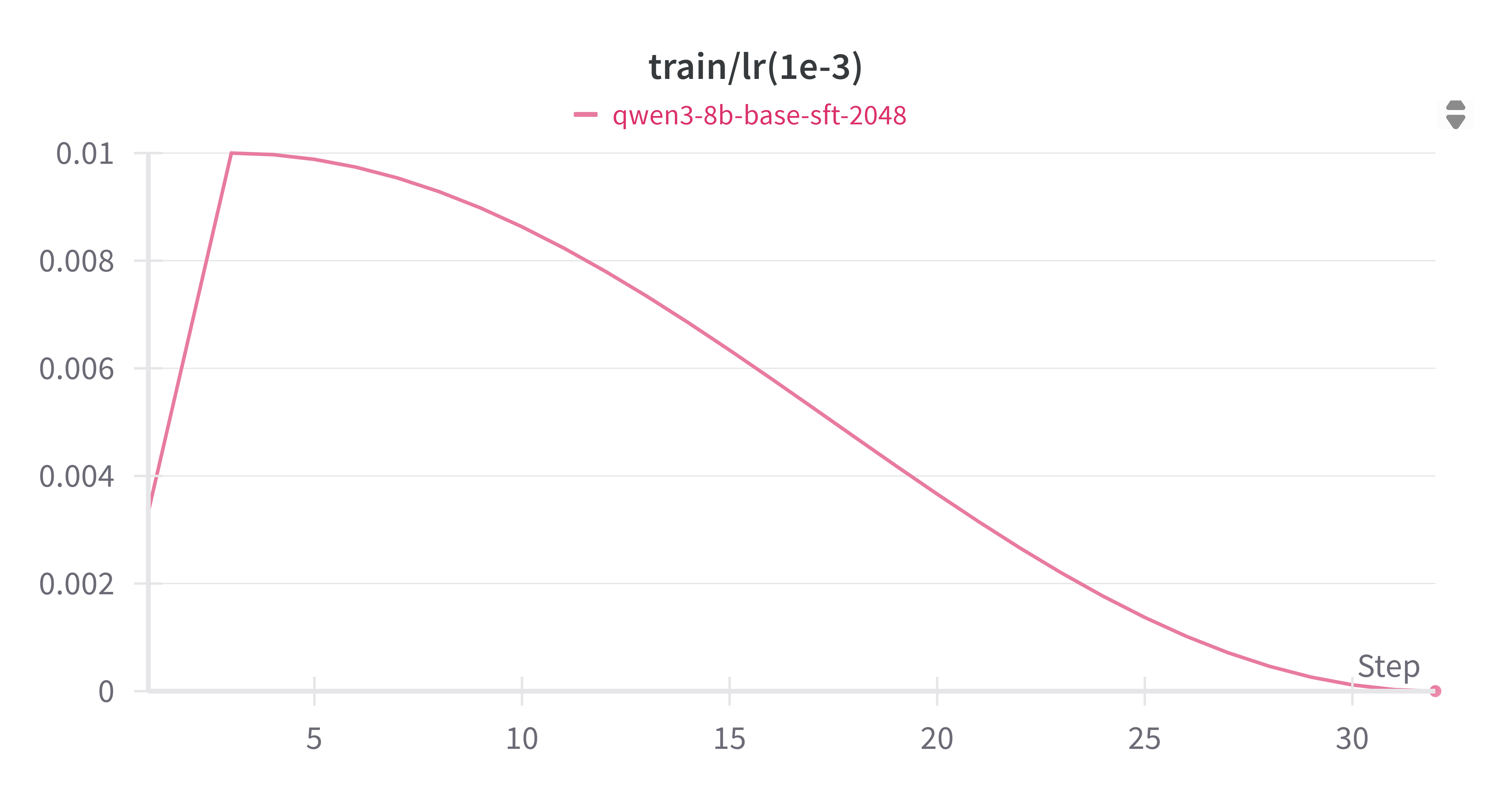
We used a cosine annealing schedule with warm-up. This helped stabilize training early and encouraged convergence later.
In summary, SFT successfully prepared the model with foundational math reasoning skills. While more training could further reduce loss, the cold start was sufficient for entering the GRPO phase.
4. GRPO Training Process and Analysis
GRPO, a reinforcement learning-based policy optimization method, refines model behavior using reward feedback. We used the run_qwen3-8b_simplerl_grpo_lora.sh script.
4.1 GRPO Training Configuration
Key settings:
- Algorithm: GRPO (
algorithm.adv_estimator=grpo) - Train File:
simplerl level5 - Validation File:
gsm8k test - Batch Size: 32
- Max Prompt/Response Lengths: 1024 / 8192
- Model Path: HuggingFace snapshot
- LoRA Rank: 64, Alpha: 32
- Actor LR: 5e-7
- PPO Mini/Micro Batch Size: 8 / 2
- KL Loss: enabled, coefficient 0.001
- Gradient Checkpointing: enabled
- Parameter Offload: ref only
- Rollout Settings: max tokens = 32748, TP size = 4, memory utilization = 0.6
- GPUs: 8
- Project/Experiment Names:
qwen3-8b-grpo,qwen3-8b_simplerl_grpo_lora
4.2 GRPO Training Results
4.2.1 Actor KL Loss
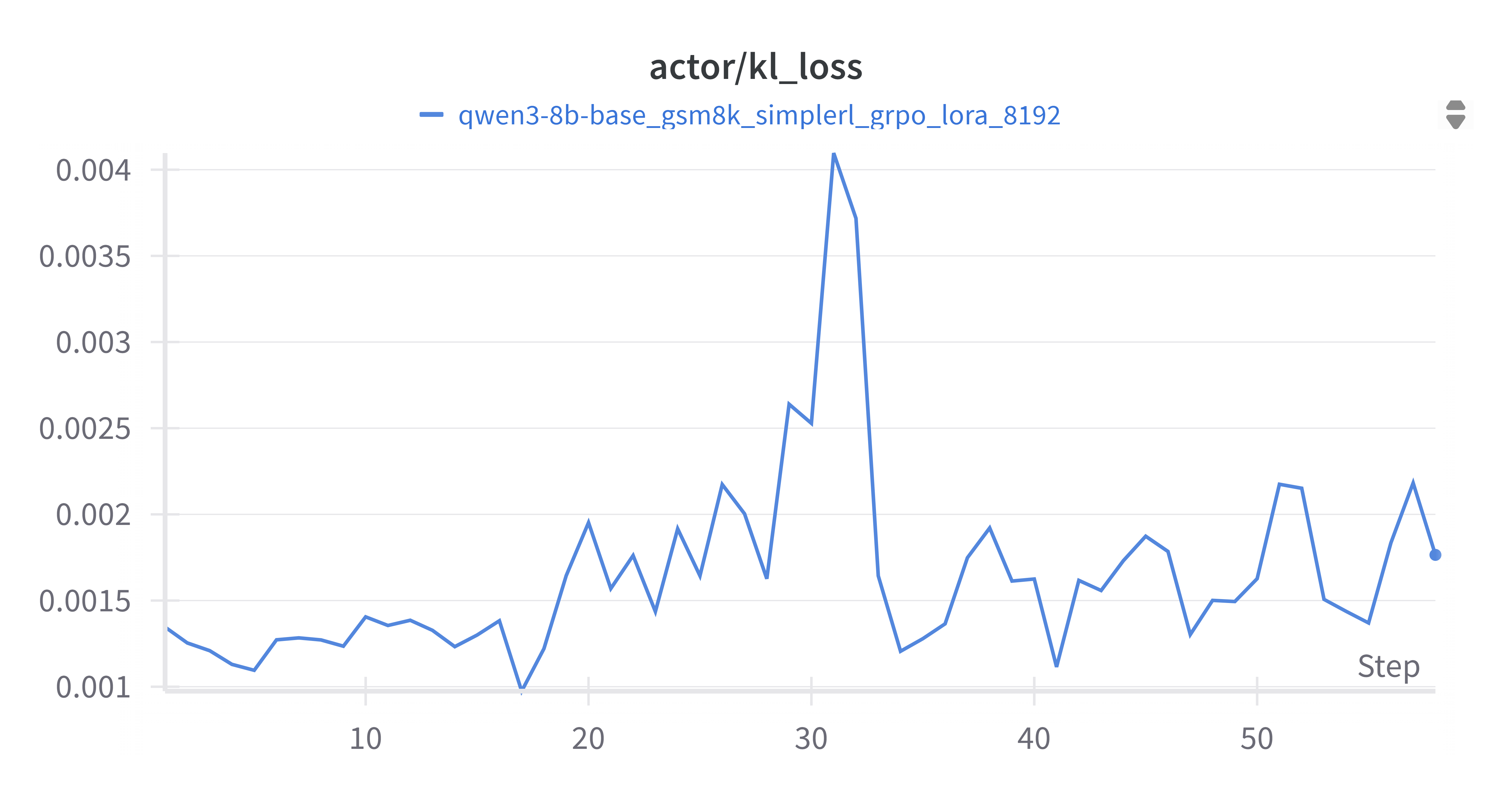
KL loss remained in the 0.001–0.004 range, indicating stability and bounded policy updates.
4.2.2 Critic Score Mean
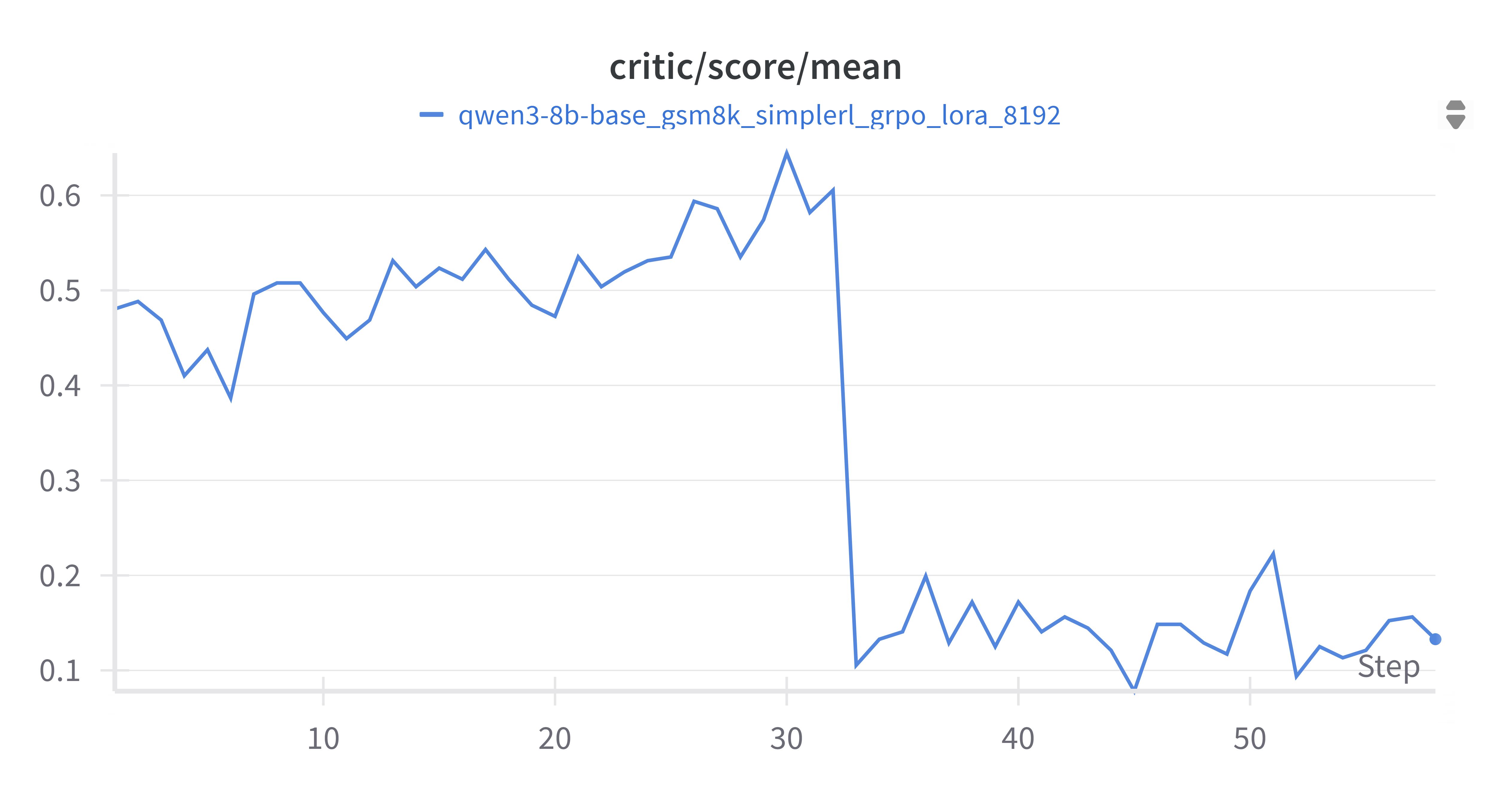
A noticeable drop occurred after switching datasets to harder samples (level 5), stabilizing at ~0.1–0.2.
4.2.3 Validation Mean Reward
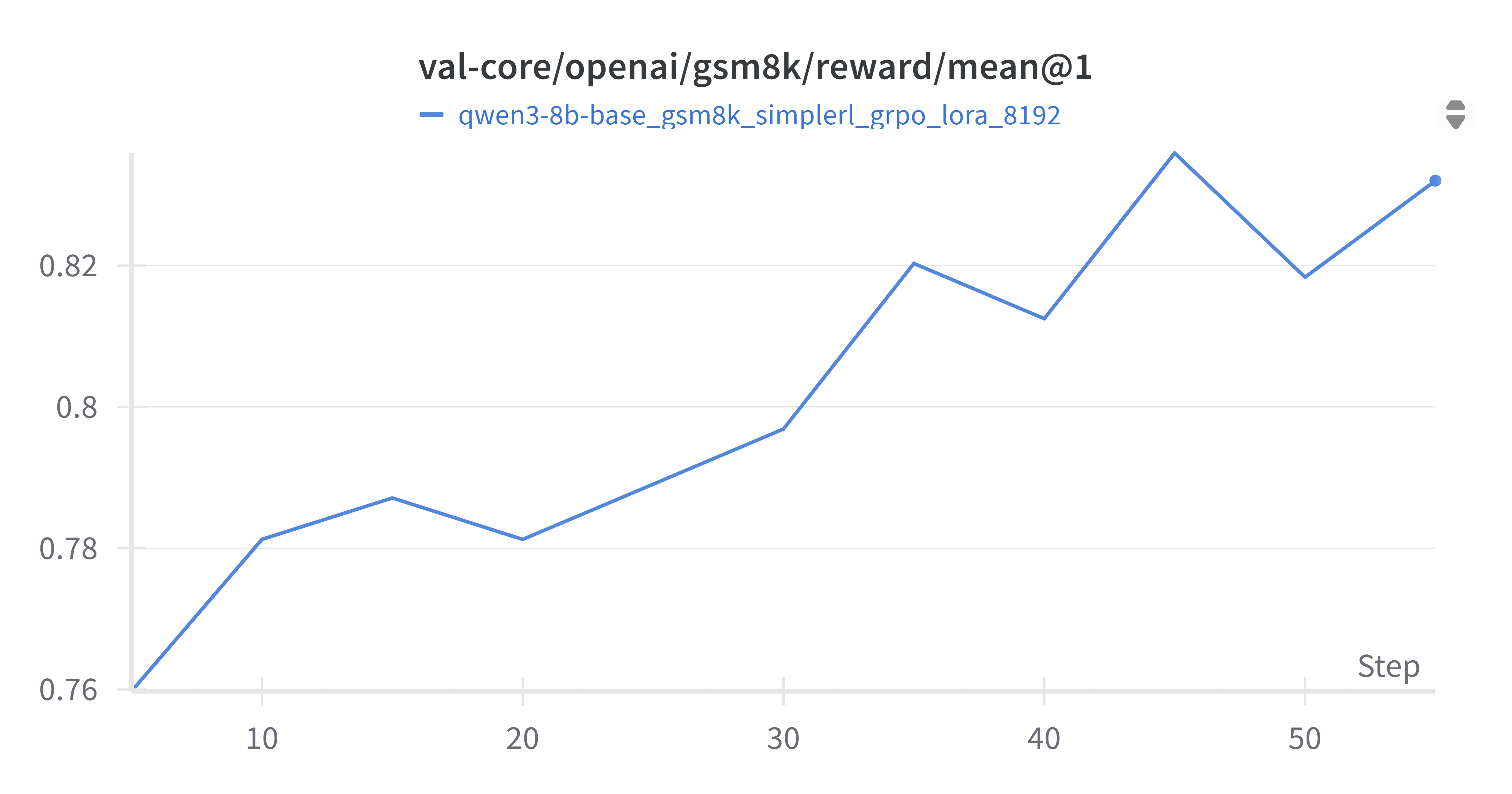
Validation reward improved from ~0.76 to ~0.83, confirming enhanced output quality.
4.2.4 Actor PG Loss
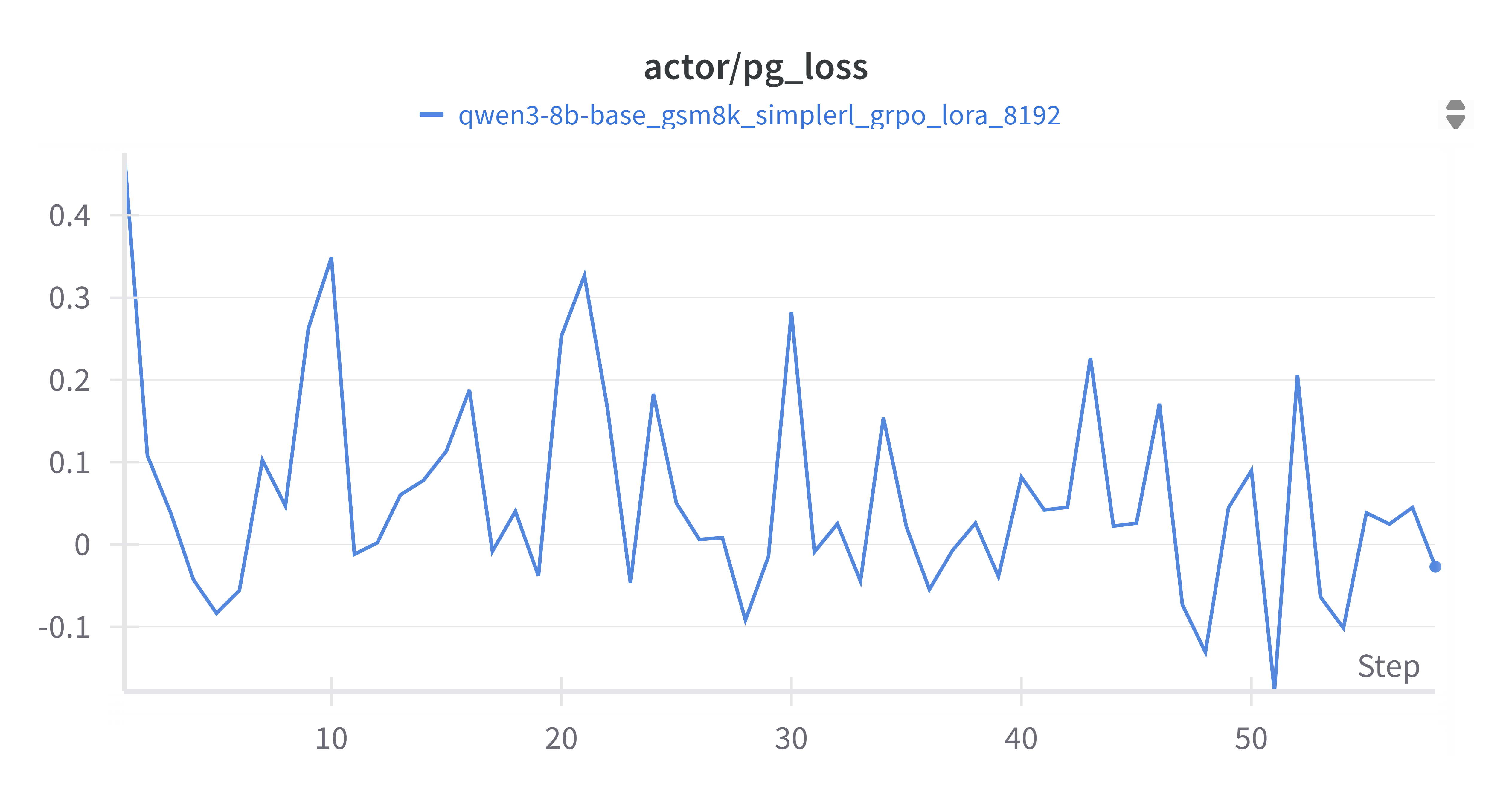
PG loss showed high variance—typical of policy gradient methods—but ultimately led to reward gains.
4.2.5 Critic Returns Mean
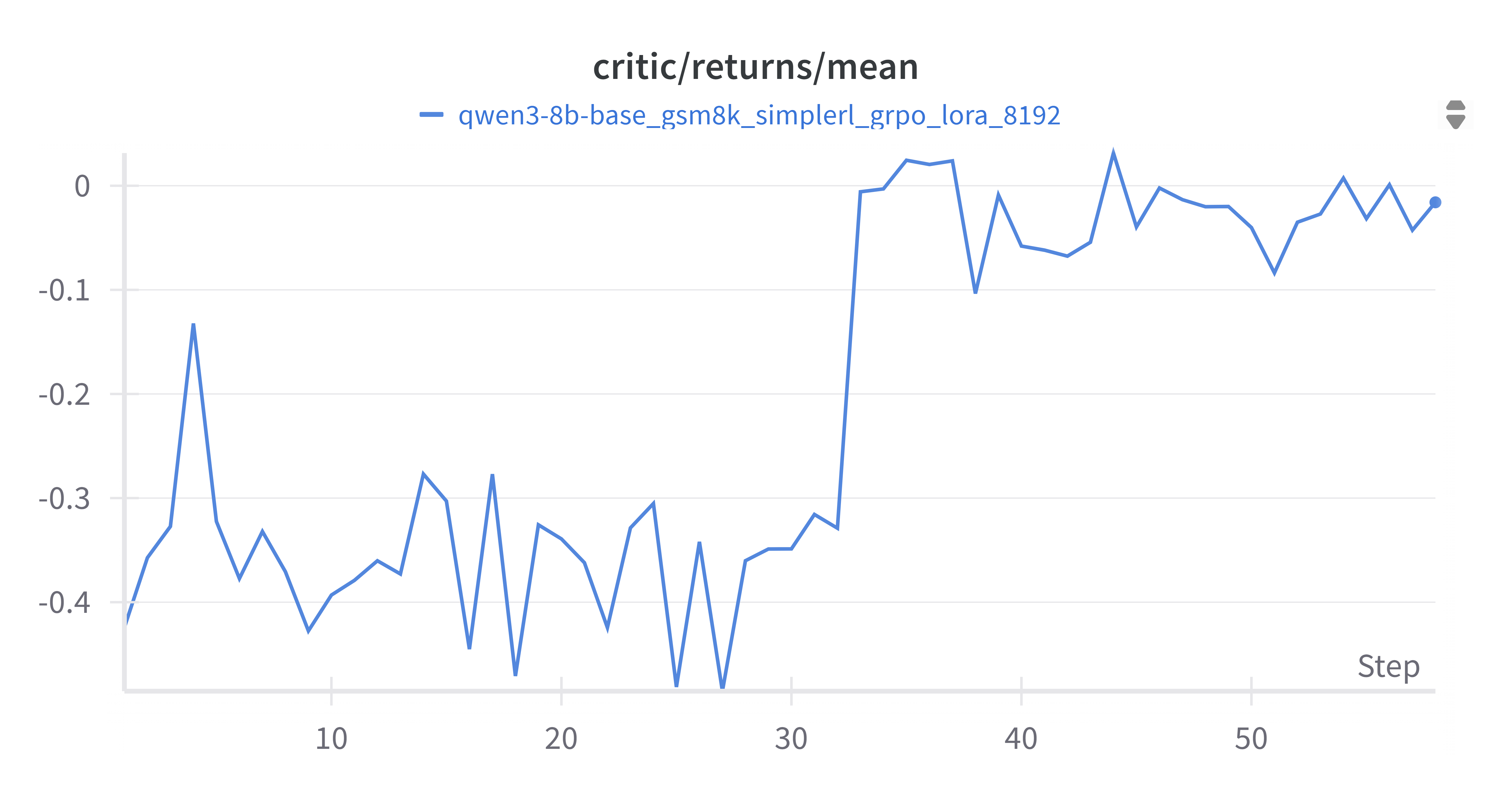
Returns increased from -0.4 to near 0.05, reflecting better return estimation after adapting to harder data.
GRPO was effective in enhancing model behavior and performance.
5. Final Evaluation Results
| Model | GSM8K | AIME24 | Notes |
|---|---|---|---|
| Qwen3-8B-Base | 61.92 | 10 | Repetition issues on AIME24 |
| Qwen3-8B-Base-sft | 63.48 | 13.3 | Minor GSM8K gain; AIME24 unchanged |
| Qwen3-8B-Base-sft-grpo | 83.59 | 16.7 | Major gains on both datasets |
Key Takeaways:
- The base model struggled with AIME24 due to repetition.
- SFT marginally improved GSM8K, not AIME24.
- GRPO brought large GSM8K gains and resolved repetition on AIME24.
5.1 Analysis of Base vs. RL-Fine-Tuned Model Outputs on the AIME 24 Dataset
Problems where the Base model was wrong but the RL-trained model was correct: 14, 19
Problem 14
Find the largest possible real part of
$$ (75+117i)z+\frac{96+144i}{z}!, $$
where $z$ is a complex number with $|z|=4$.
| Aspect | Base Model ① | GRPO Model ② |
|---|---|---|
| Final answer | 600 (incorrect) | 540 (correct) |
| Real-part simplification | Treats the expression as $\operatorname{Re}[(75+117i)z]+\operatorname{Re}[(96+144i)/z]$. Critical error: expands $(75+117i)(4\cos\theta+4\sin\theta i)$ as $(24\cos\theta+36\sin\theta i)+(36\cos\theta+24\sin\theta i)$, giving coefficients 360, 528 that are too large; also mishandles $i^{2}=-1$. |
Obtains $\operatorname{Re}=324\cos\theta+432\sin\theta$ but the correct form is $324\cos\theta-432\sin\theta$. |
| Maximization | Directly writes $\cos\theta=\dfrac{528}{\sqrt{360^{2}+528^{2}}}=\dfrac{132}{119}$ and similarly for $\sin\theta$, producing impossible trigonometric values (> 1), thus hiding the earlier coefficient error. |
Correctly computes the maximum as $\sqrt{324^{2}+432^{2}}=540$ with $\cos\theta=\tfrac35,;\sin\theta=\tfrac45$. |
Take-away ① mishandles $i^{2}$ and coefficient consistency. ② sign error in the real part, yet both incorrect and correct formulas share the same maximum 540 by coincidence.
Problem 19
Determine the number of triples of non-negative integers $(a,b,c)$ satisfying
$$ a+b+c=300 $$
and
$$ a^{2}b+a^{2}c+b^{2}a+b^{2}c+c^{2}a+c^{2}b = 6{,}000{,}000. $$
| Aspect | GRPO Model ① | Base Model ② |
|---|---|---|
| Final answer | 601 (correct) | 0 |
| Key algebraic step | Uses the identity $a^{3}+b^{3}+c^{3}-3abc$$=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca).$ With $a+b+c=300$, derives $50(a^{2}+b^{2}+c^{2})+abc=2{,}500{,}000$ |
Writes $6{,}000{,}000$$=(a+b+c)(ab+ac+bc)-3abc $ and rearranges to $a^{2}+b^{2}+c^{2}$ $=90{,}000-\frac{12{,}000{,}000+6abc}{300}$ |
| Enumeration strategy | Double loop over (a,b); compute (c=300-a-b) and test the derived equation. |
Tests whether $a^{2}+b^{2}+c^{2}$ is an integer via float.is_integer(), which is numerically fragile and not directly tied to the original constraint, leading to zero solutions. |
1# Code 1 – GRPO model
2count = 0
3for a in range(301):
4 for b in range(301 - a):
5 c = 300 - a - b
6 if 50 * (a**2 + b**2 + c**2) + a * b * c == 2500000:
7 count += 1
8print(count) # 601
1# Code 2 – Base model
2count = 0
3for a in range(301):
4 for b in range(301 - a):
5 c = 300 - a - b
6 abc = a * b * c
7 a2_b2_c2 = 90000 - (12000000 + 6 * abc) / 300
8 if a2_b2_c2.is_integer() and a2_b2_c2 >= 0:
9 count += 1
10print(count) # 0
Take-away
① leverages the exact algebraic constraint and a simple enumeration.
② invents an unrelated test criterion, ignoring equality, and suffers from floating-point issues.
Observations and Reflections
- Both models show the right overall approach but often slip on algebraic manipulation—most commonly sign errors, incorrect coefficients, or missing parentheses.
- The Base model is prone to inconsistent derivations, so an early mistake breaks the entire reasoning chain.
- RL fine-tuning noticeably improves coefficient/sign accuracy and overall symbolic consistency.
- Introducing step-by-step formula derivation during SFT or RL could further raise mathematical reasoning fidelity.
- Even a small, targeted SFT dataset—focusing on simple identities or unit-coefficient exercises—might yield significant gains.
6. Conclusion and Future Work
This SFT+GRPO training was a success. By combining supervised and RL training, we significantly boosted Qwen3-8b-base’s performance on math tasks.
Key insights:
- SFT lays the foundation for reasoning skills.
- GRPO fine-tunes behavior via reward alignment.
- Proper LR scheduling, KL control, and validation metrics are critical.
Future directions:
- Explore DAPO or other advanced RL algorithms
- Expand dataset diversity and quality
- Scale to larger hardware setups
- Refine hyperparameter search
This experiment showcases how SFT+GRPO can effectively enhance LLMs for domain-specific reasoning tasks.
Appendix: Training Notes
- Memory Estimation: BF16 + FP32 Adam without gradient checkpointing needs ~7–8× param size. A 7B model may need ~100GB.
- Gradual Output Length Scaling: Start small and gradually increase
output_seq_lento maximize memory usage. - Debugging Configs: Expect issues during training; tune
max_num_batched_tokensfor vLLM profiling stages. - Monitoring is Key: Track loss, KL, reward, LR, grad norm using tools like wandb to catch issues early.